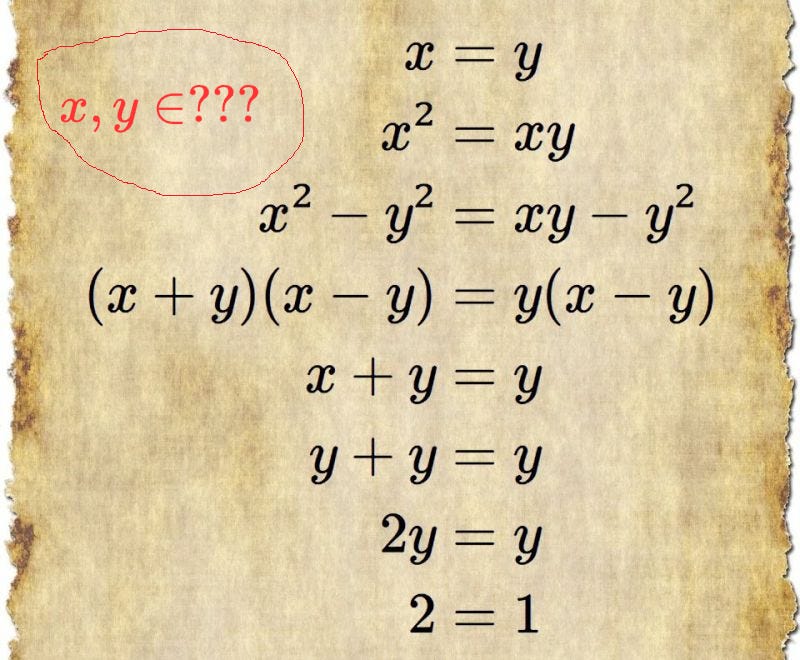A Mathematical Expression Without Context Is Just Symbolic Noise

I often come across challenges like this on my LinkedIn feed, so I thought I would share a brief comment in the spirit of Quantum Formalism (QF).

From a mathematician’s point of view, these puzzles usually miss some subtle but important details. One key detail (I highlighted in red) is that when solving an equation like this, we need to know the algebraic setting in which it takes place.

The symbols 𝒙 and 𝒚 have no meaning until we specify the universe of rules they belong to. For instance, are we working within a ring, an integral domain, or a field? And beyond that, what is the characteristic of the ring or field? Is the structure commutative?

So next time you come across a challenge like this, remember that context defines the rules, and in mathematics, the rules define the meaning. Indeed, properties that hold in familiar algebraic structures such as the ring of ordinary integers or the real numbers do not necessarily hold in other, more abstract algebraic systems.

Credits to Jack Raifer Baruch for the original challenge image and thanks to Scott Ogden and Patrick Nicolas for making me aware of Jack’s post.

👉𝑪𝒐𝒏𝒔𝒊𝒅𝒆𝒓 𝒋𝒐𝒊𝒏𝒊𝒏𝒈 𝒐𝒖𝒓 𝒖𝒑𝒄𝒐𝒎𝒊𝒏𝒈 𝑨𝒃𝒔𝒕𝒓𝒂𝒄𝒕 𝑴𝒂𝒕𝒉𝒔 101 𝑩𝒐𝒐𝒕𝒄𝒂𝒎𝒑 𝒕𝒐 𝒆𝒙𝒑𝒍𝒐𝒓𝒆 𝒕𝒉𝒆𝒔𝒆 𝒊𝒅𝒆𝒂𝒔 𝒊𝒏 𝒈𝒓𝒆𝒂𝒕𝒆𝒓 𝒅𝒆𝒑𝒕𝒉: https://quantumformalism.academy/abstract-maths-101-bootcamp

Have a great rest of the week ahead!

Bambordé

QF Academy team